Godot Engine – How to remap a range of numbers

Last Updated on 30. September 2022 by Victor Karp

The explanation of range remapping in this article is universally applicable to every use case where value remapping is required. Towards the end of this article we’ll take a look at how to implement the formula as a function in the Godot game engine.

If you are just here to understand how range remapping works in Godot and don’t want to write your own function, you can simply use the built-in range_lerp() function in Godot 3.x or remap() in Godot 4.x.

A use case for value remapping

Let’s say you create a survival game where the player has to eat to survive. At 30% hunger his base health regeneration rate of 3/sec starts to decrease. If the hunger hits 90%, the regeneration is at a maximum of negative 1/sec, which causes the player to lose health.

You now want to find out what the regeneration rate for any value between 30% and 90% hunger is.

We’ll call the percentage of hunger the player has right now value. The hunger’s range from 30 to 90 is InputA and InputB. The regeneration values from 3 to -1 are OutputA and OutputB.

InputA and OutputA (30 and 3) and InputB and OutputB (90 and -1) are paired up.

To figure out the resulting regeneration value, we can use this formula:

result = (value - InputA) / (InputB - InputA) * (OutputB - OutputA) + OutputA

So, if the player is 78% hungry, the formula looks like this:

-0.2 = (78 - 30) / (90 - 30) * (-1 - 3) + 3

The formula is working, but how?

If you are a visual learning type like me, you might not get what’s happening there at first. But it’s actually quite simple if you deconstruct each step. Let’s begin with visualizing the values.

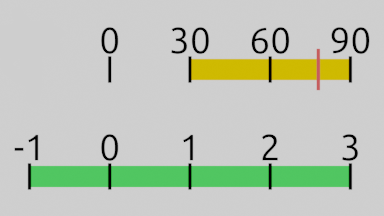
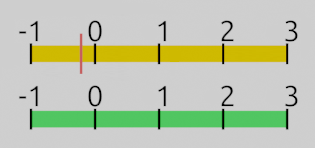
The value range for the player’s hunger is yellow, the one for the regeneration value is green. The current hunger level is indicated by the red bar. I’ve aligned the bars in a way that 0 and the maximum values line up. Keep focused on the red bar to understand how the input value is changing with every operation.

Now we’ll split the formula into four steps.

A) (value - InputA)
B) divided by (InputB - InputA)
C) multiplied by (OutputB - OutputA)
D) plus OutputA

A) (value – InputA) moves the yellow bar’s start to 0. Imagine grabbing the bar and moving it 30 units to the left. The values now range from 0 – 60. Our current hunger value of 78 is now offset by -30 too, which is 48.

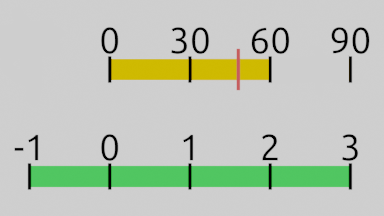
B) (InputB – InputA) yields the yellow hunger bar’s total length. In our example that would be 90 – 30, which is 60. If we divide the entire yellow bar by 60, its length becomes 1. This scales the hunger value from 48 down to 0.8. The hunger value has been normalized, because its new minimum and maximum value (the yellow bar) is between 0 and 1.

C) OutputB – OutputA is the total length of the green bar (-1 – 3), which is -4. If we multiply our yellow bar with the green bar’s total size of -4, they’ll have the same size, but the yellow bar flips sides. The hunger value (0.8) has been scaled by -4 too and is now at -3.2.

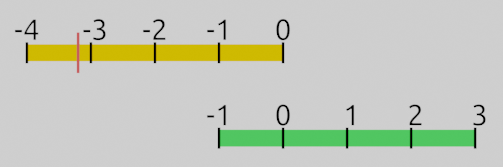
D) + OutputA aligns the yellow bar with the green one. We add the green bar’s OutputA value, which is 3, to the yellow bar. All values inside the yellow bar are shifted by 3. The two bars are fully matched up now and our hunger value has moved from -3.2 to its final position at -0.2. We now know that a hunger value of 78% causes the regeneration rate to fall from 3/sec to -0.2/sec.

Creating the remap_range() function in Godot

We’ll now write this as a remap_range() function in Godot that gives the equation’s outcome back as a return value so we can reuse it with any numbers we choose.

func remap_range(value, InputA, InputB, OutputA, OutputB):
    return(value - InputA) / (InputB - InputA) * (OutputB - OutputA) + OutputA

Important: Make sure to enter the input variable as a float when you call this function or the resulting value will be wrong due to rounding errors. If your value doesn’t have a floating point value, just add .0 to it.

Visit the Godot Tutorial main page for more Godot tutorials.